超幾何分布とは何かについては、前回解説しました。
今回は、超幾何分布と二項分布およびポアソン分布はどういった関係性があるのか解説します。
二項分布との関係
結論から言うと、二項分布は超幾何分布の極限分布です。
超幾何分布の式は、要素の数N個(不適合品a個)からランダムにn個を抜き取った時、その中に含まれる不適合品の個数がx個となる確率と考えれば以下の式になります。
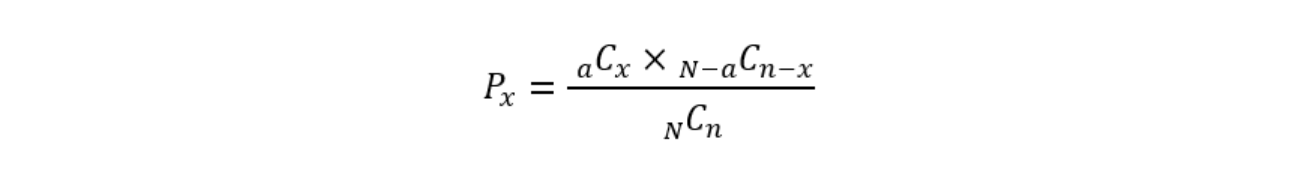
一方、二項分布は以下の式になります。
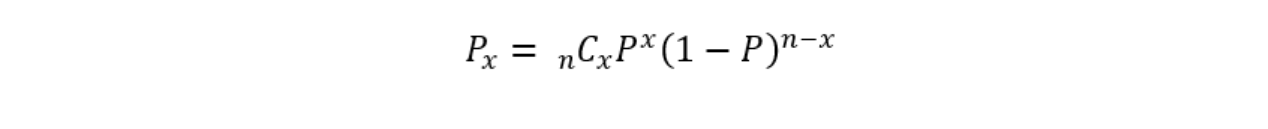
ここでのPは不適合品率を示しており次のように表すことができます。
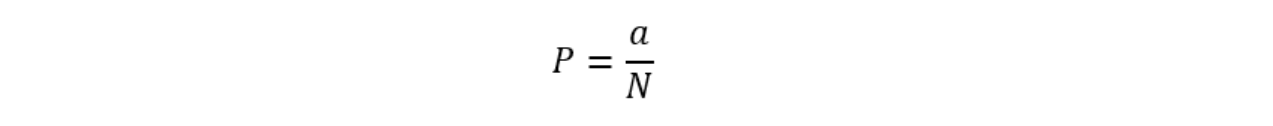
両者を見比べて考え方の違いがわかりますでしょうか。
簡単に言えば、
二項分布では取り出す際に生じる母数の個数の変化を無視し不良率の変化を一定としている
ということです。
つまり、超幾何分布の式が厳密だけど、取り出し個数が多いとその影響は少ないよね。
だから、一定で近似できるでしょ!っていう考え方です。
よって、二項分布は超幾何分布の式においてPを一定として取り出し個数を∞に近似した極限分布です
ポアソン分布との関係
ポアソン分布は、二項分布において期待値nPを一定とした状態で、
サンプル数を∞に近似した極限分布となります。
ポアソンの極限定理とも呼び次のように表せます。
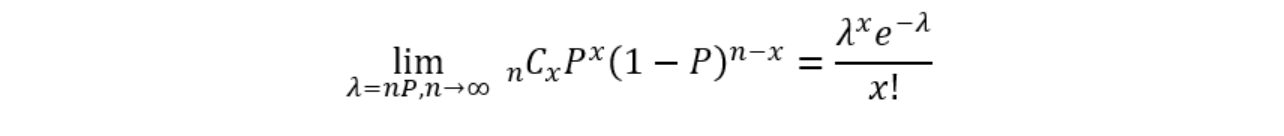
それでは導出してみましょう。

ここまでできたらあとはネピアの数の近似を使って導出は完了です。
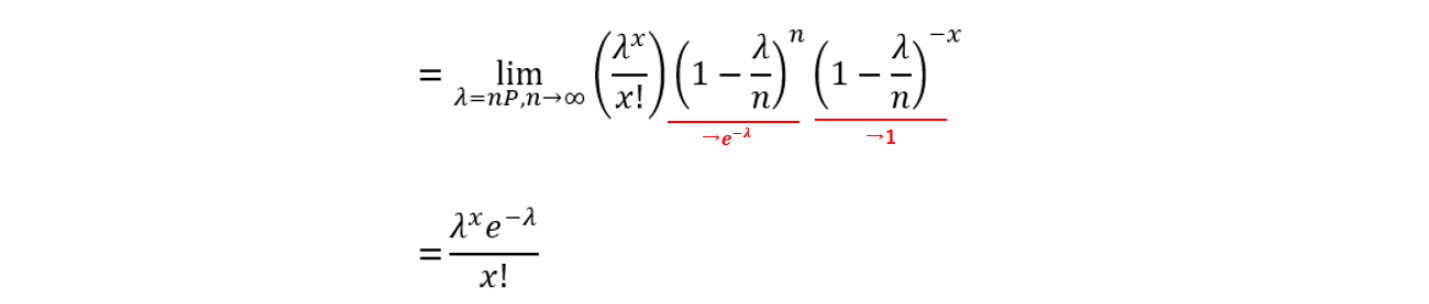
導出できました。
まとめ
超幾何分布と二項分布およびポアソン分布の関係は次のように説明できます。
二項分布
超幾何分布において、要素数がかなり大きい場合は不良率はサンプルを抜き取っても
初期値と変わらないと考えられるよねっていうのが二項分布
ポアソン分布
二項分布からさらに、抜き取るサンプル数の個数がかなり大きく、不良個数がかなり小さい時は
任意のポアソン分布に落ち着きますということです。
実用的に、超幾何分布を二項分布やポアソン分布に当てはめられるか判断する基準が
N:要素数、n:抜き取り個数、x:抜き取った中の不具合品個数

となっています。
QC検定の勉強をしている方向けに、過去問 第23回 の大門2を題材にして
統計データの仮説検定についても解説しているので、こちらも良ければ参考してください。





コメント