第23回大門2解説
QC検定2級の題材でもある統計データの仮説検定について、第23回の大門2を題材に解説します。
問題は社内で211.0±6.0に設定されている特性値Qを満足させるための改善活動についてです。
具体的な例に落とし込んだ方が分かりやすいので、ここではこの会社を板材を生産している会社とし、
特性値Qは、板材の縦の寸法値とします。問題設定について図示すると下記のような感じです！
では、問題を解いていきます。
まず、今回工場から生産された板材の特性値Qは正規分布型であり、対策前の偏差σは2.0だそうです。
この正規分布型であることが重要です。
正規分布型でない場合は、仮説検定に用いられる統計量（t分布、F分布なども含める）は使えません！
今回は、正規分布型だったそうなのでχの2乗分布を使います！
1問目で、その値が問われているので求めましょう。
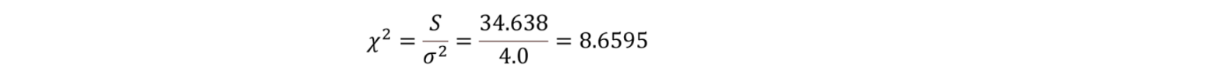
算出できました！
しかし、定義式に当てはめただけで求めても知識は広がりません。
χの2乗の値は、どういうものか考える必要があります。
分母が、対策前の偏差の2乗であり、分子が対策後の20個抜き取った板材の特性値Qの平方和です。
平方和の定義式は、下記でした。
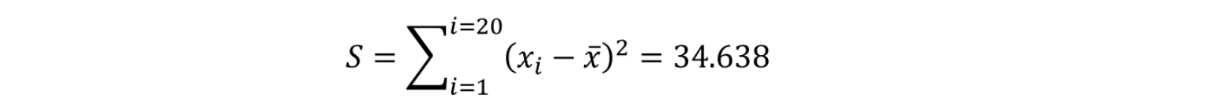
つまり、サンプルのバラつきが大きかったり、データ個数が大きくなると大きくなる数字です。
だから、該当の値を調べる際に使う付属の表では自由度(データ個数)によって値が違うんですね！
そして、χの2乗の定義式は、分母も分子もバラつきを示す指標なので、
χの2乗の値が大きい ⇒ 以前と比べてバラつきが大きい
χの2乗の値が小さい ⇒ 以前と比べてバラつきが小さい
ということになります。
続いて、信頼率95％での母分散を求めます。
母分散を求める際、使用する式はχの2乗の定義式で母分散について式変形した下記の式です。
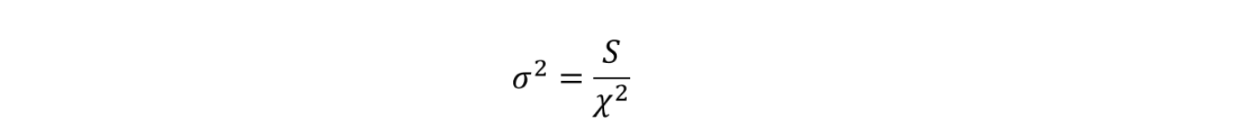
この式をいちいち単独で丸暗記しないようにしましょう！
自由度19で下側2.5%(0.025)、上側97.5%(0.975)の χの2乗値を付属の表から探します。
χの2乗の表より、自由度19で確率Pが0.975の χの2乗値は8.91、 0.025χの2乗値は32.9です。
これを代入して、母分散を推定します。
χの2乗値が大きい方が、バラつきが大きい つまり、母分散が大きくなります。
以上より、母分散の上限値は3.888、母分散の下限値は1.053となります。
さて、分散の次は母平均μに関しての検討です。母平均については検定量ｔを使います。
検定量ｔの定義式は、、
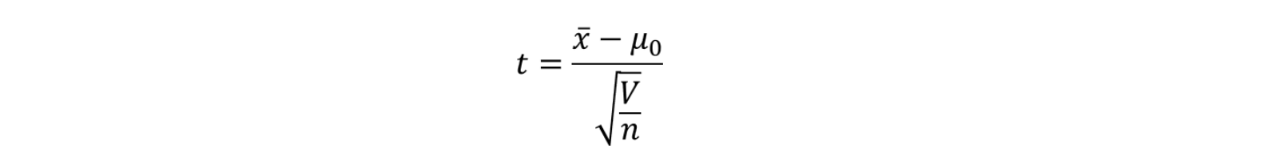
検定量tが大きいことは、母集団とサンプルとの差が大きいことを表しています。
そのため、例えばサンプル平均と母平均が近くなれば小さくなりますし、
サンプル数大きくしているのに標本平均と母平均の差が同じであれば、検定量tは大きくなります。
それでは、今回の問題での検定量tを算出しましょう。
まずは、分散値を算出します。
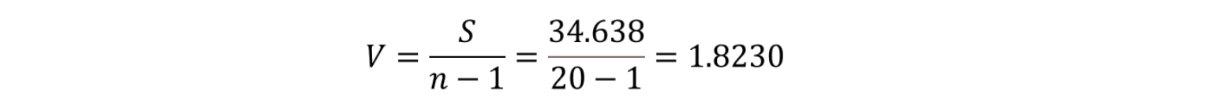
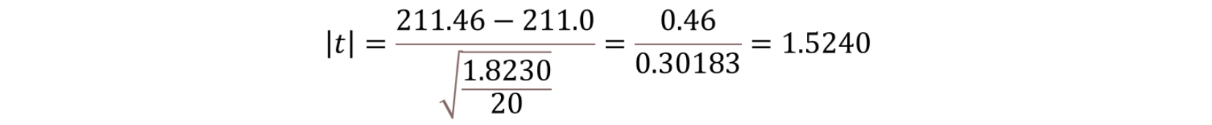
続いて、信頼上限値と信頼下限値を算出します。
検定量tの定義式から変形して、平均値の上限値と下限値を求める式は次の通りになります。
対策後の母標準偏差は、分散Vをすでに算出しているので次のように求められます。
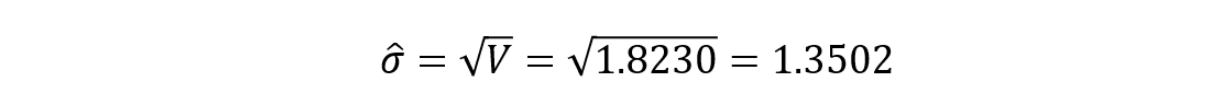
工程能力指数Cpは、規格範囲値を6σで除して求められるので次のように求められます。
ちなみにですが、工程能力指数に対する工程の評価は次のようになります。
こちらで判断したところ、今の工程能力は「十分満足している」ということになります！
コメント