超幾何分布とは?
超幾何分布は、二項分布とポアソン分布の基礎となるものです。
「超幾何分布」って名前は知らないけど、高校数学でやったことある!っていう人が多いと思います
では早速、超幾何分布をお見せします!
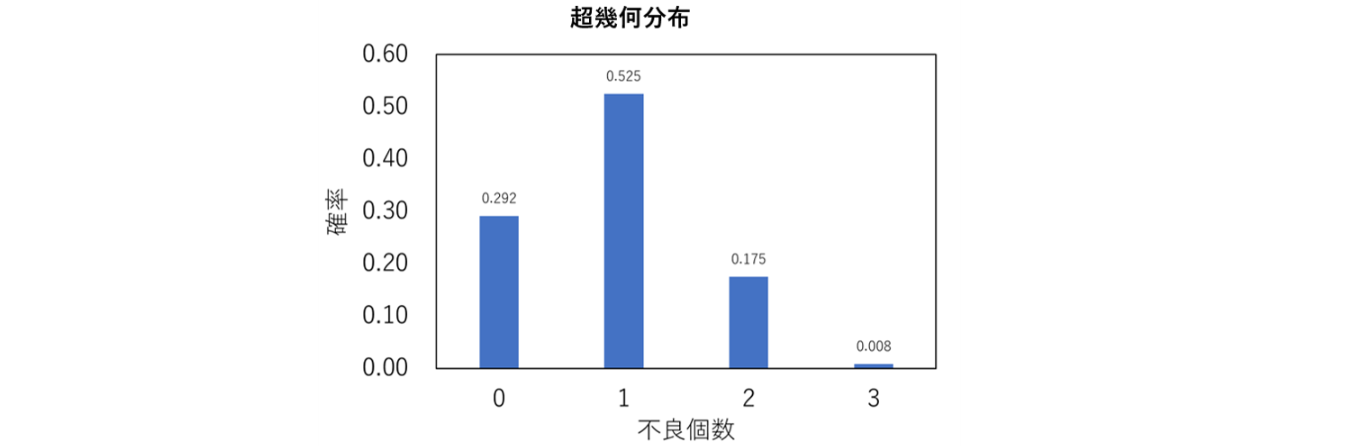
これは3個の不良品が含まれている10個の中から3個取り出すとき、
含まれる不良品の個数を確率で示したものです。
つまり、 10個 (不良品3個を含む)からピッキングした3個のボルトの中に不良品が
0個となるのは 29.2 % (0.292)
1個となるのは 52.5% (0.525)
2個となるのは 17.5% (0.175)
取り出した3個が全部不良品となるのは 0.8% (0.008)
ということになります!
じゃあ、ここでクイズです!
不良品の個数が4個となるのは何%でしょう???
取り出したの3個だけですので、0%ですね笑
ここで、すでにお気づきの人がいるかもしれませんが、「超幾何分布」は高校数学でやってます。
確率(順列・組合せ)みたいな項目だったと思います。
えっ、もう覚えてないや… って方も分かるように深掘りしていきます。
超幾何分布は、離散分布の仲間です。上の図でも示したようにx軸に1.1個とか存在しないですからね!
要素の数N個(不良品a個)の中からb個取り出すとき、そのb個の中に不良品x個含まれている確率は
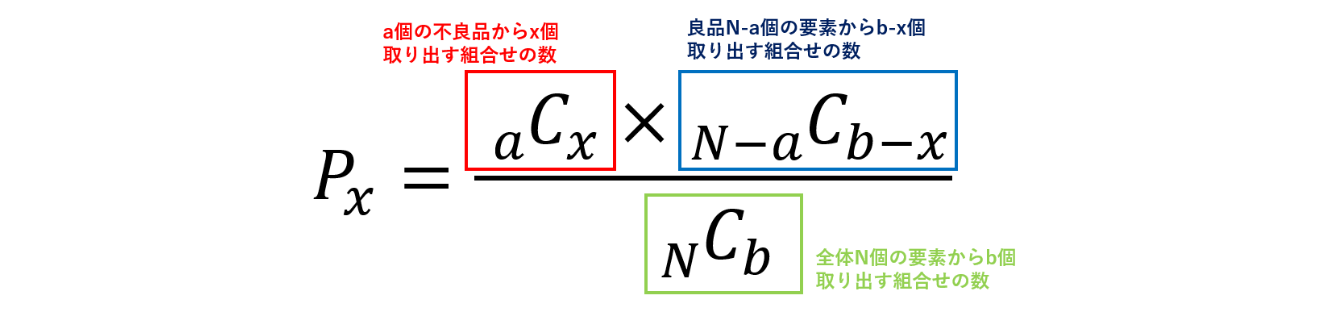
と表すことができます。これが、超幾何分布と呼ばれています。
期待値の導出方法について
超幾何分布の期待値は、
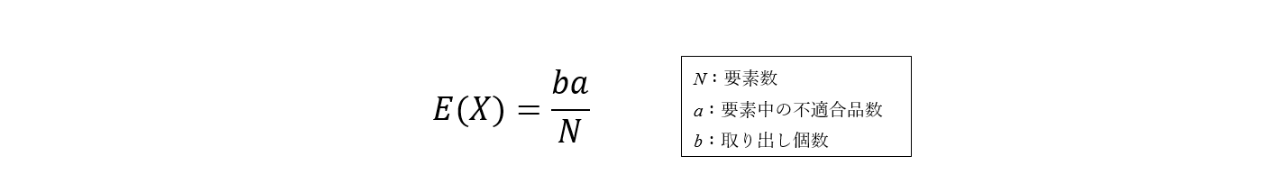
で表すことができます。
では、期待値を導出していきましょう。
期待値は、それぞれの不良個数の場合のときの、(個数)×(その個数となる確率)の和で求められます。
つまり、式で表すと以下のようになります!
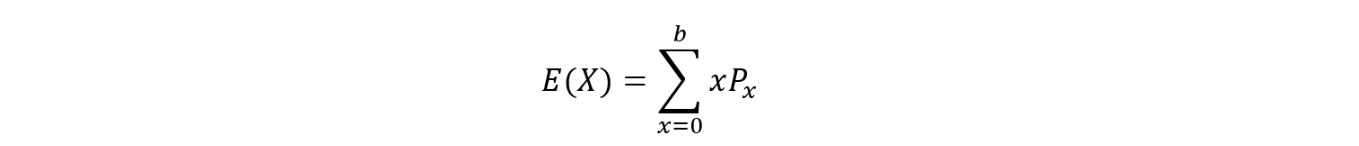
ここで、超幾何分布の式を代入することを考えてください。なんかΣが消える予感しないですよね…
実は、ここでキレイさっぱりΣを消す方法があります。
要素の数 N-1 個(不良品 a-1 個)から、b-1 個 取り出す時、
”取り出したb-1個の中に不良品が0個、1個、2個、…、b-1個となる確率をそれぞれ足したら1になる”
ことを使います!
これを数式で表すと、次ようになりますね!

さて、では準備していきましょう。Pxの中の項を変換していきます。

このような形で、Pxの分母を書き換えられますね!
この調子で、残り二つも書き換えます!
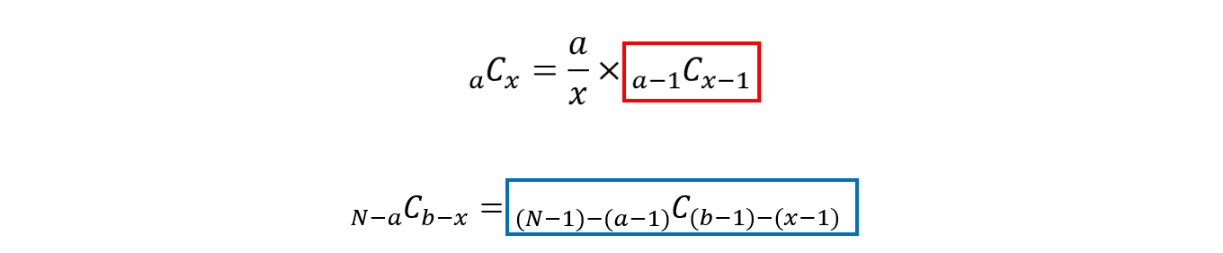
準備が整いました。では、代入しましょう!
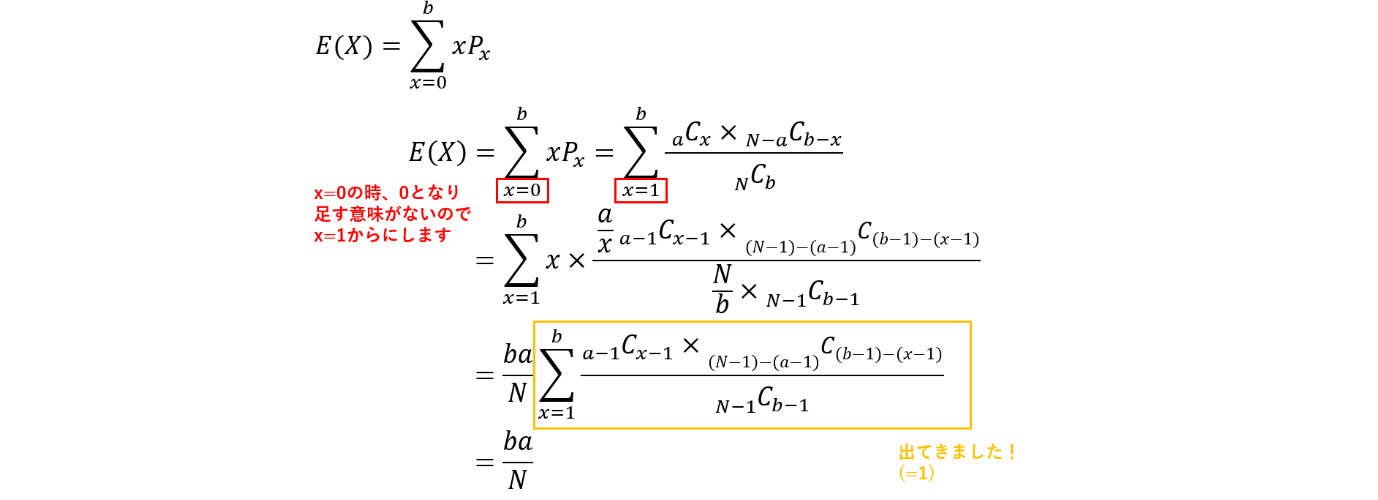
すっきり消えてきれいになりましたね!
分散の導出方法について
超幾何分布の分散は、
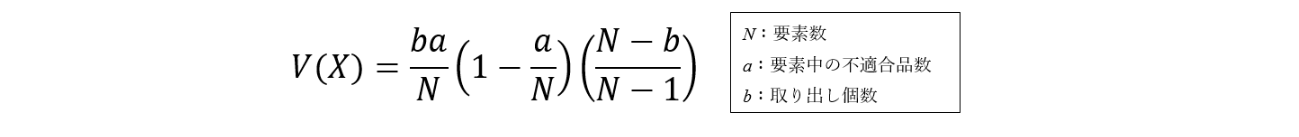
とあらわすことができます。
分散の導出方法は、期待値の導出を理解できれば簡単にわかります。
分散は、各値から期待値を引いた2乗の期待値です。
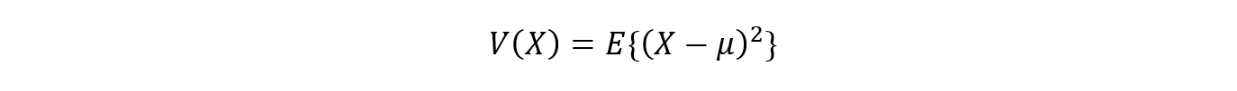
ここで、”期待値”と”平均値”を混同する方がいると思いますが、厳密にいえば異なります。
ただし、標本が母集団と一致するときは等しくなります。
この式を、書き換えると次のようになります。
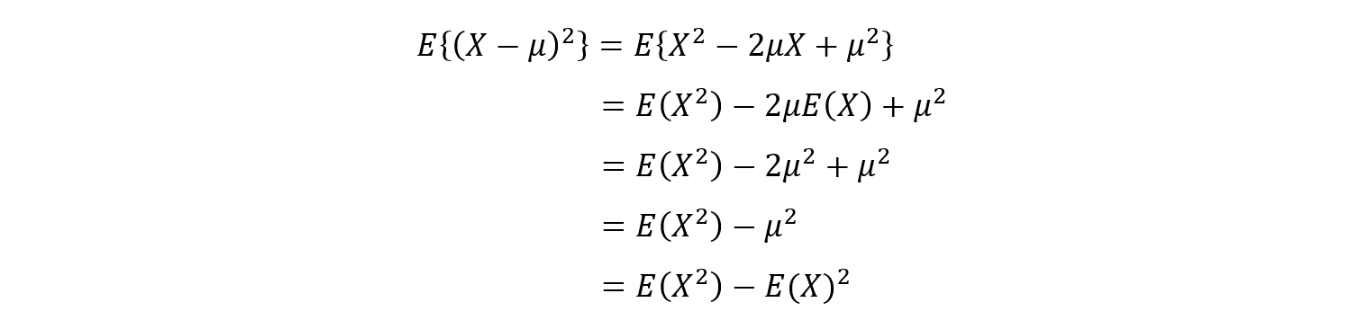
変形した意図は、先ほど求めた期待値E(X)を利用して楽して分散を求めるためです。
ここで、分からない項はE(X^2)ですよね。なので、 E(X^2)を求めていきます。
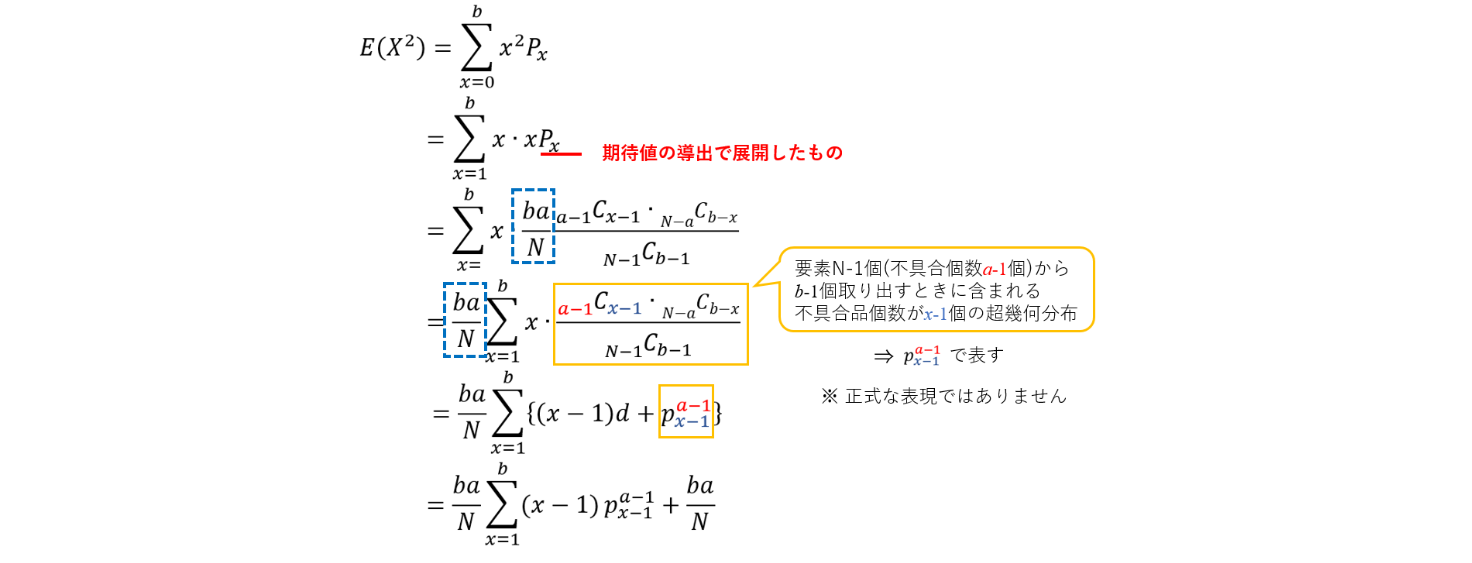
途中で(x-1)×全体から1を引いた個数の超幾何分布の式の形を作りにいっています。
これは、期待値のときと同様Σ内をキレイに計算するためです。
ここまで変形できたらあとは簡単です。

E(X^2)を求めることができました。
これで、分散は導出できそうですね。
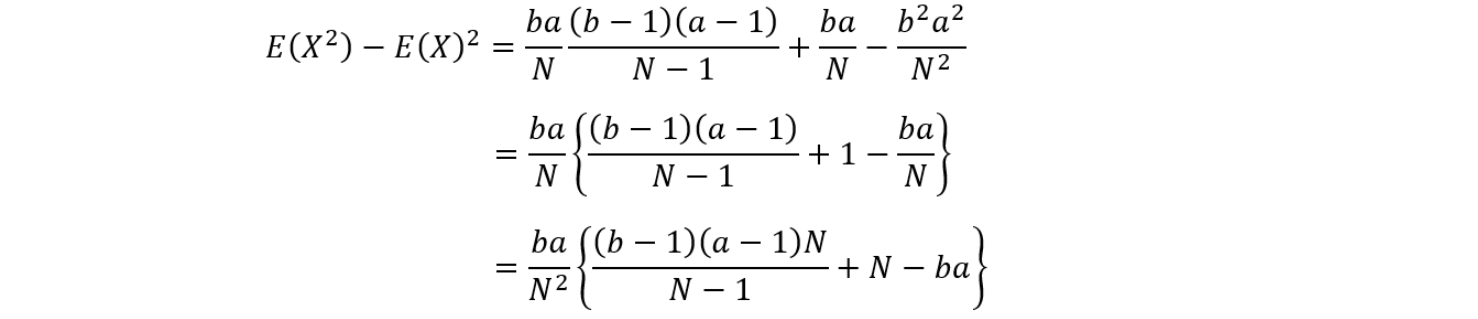
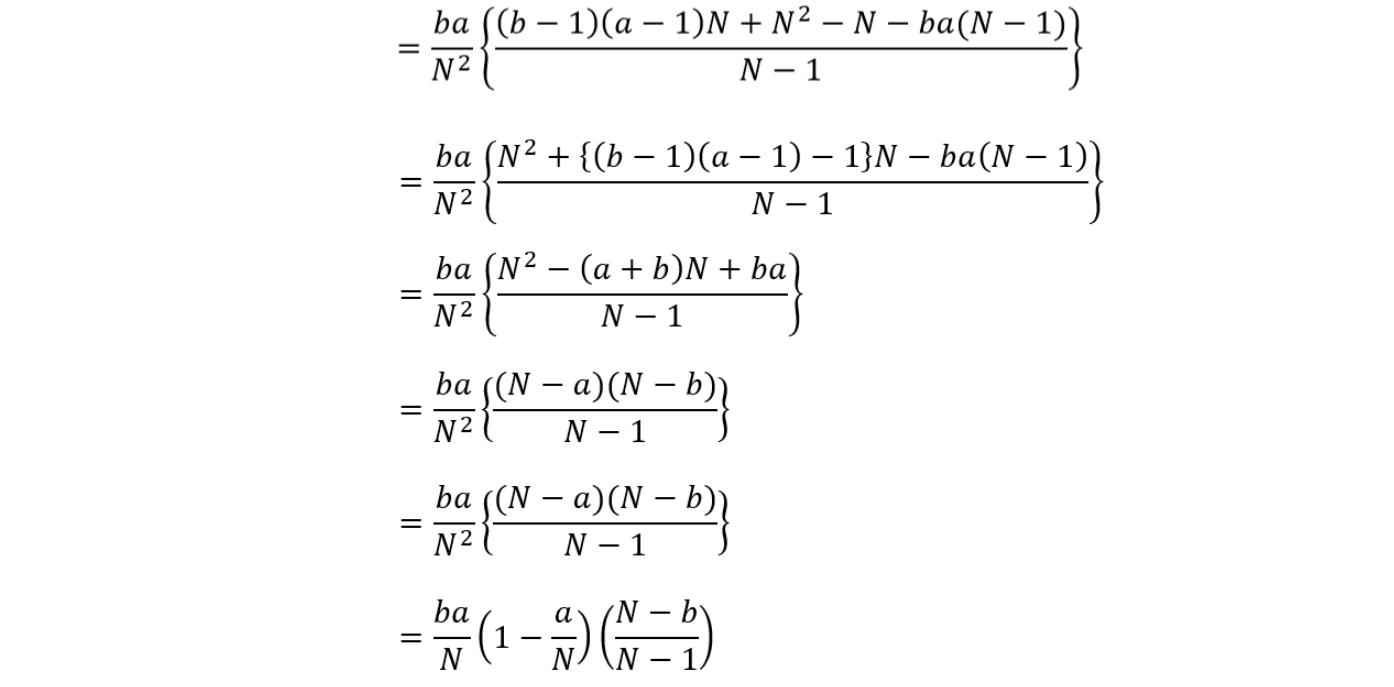
分散導出できました。
少し煩雑に見えますが、1個1個たどれば難しいことはしてないので理解できると思います。
超幾何分布と二項分布、ポアソン分布との関係については超幾分布とは(2)で取り上げます。



コメント