こんにちは、そのべです。
今回はランダムサンプリングについて解説します。
前回は、超幾何分布と二項分布・ポアソン分布の関係性について解説し、平均値と分散の導出まで行いました。
実は、ここから延長としてランダムサンプリングの理解も深めることができます。
統計学は、一本の線のように繋がっているので、1つをしっかり理解できたらその次も簡単に理解ができるんです。
ジェンガのように、土台を丁寧に作っておけば、その上は簡単に置けるのと同じですね！
なので、超幾何分布と二項分布、ポアソン分布についての理解に自信がない方は、まずは上に載せた2つの記事を先に読んでもらうといいと思います。
それでは、解説していきます！
ランダムサンプリングとは
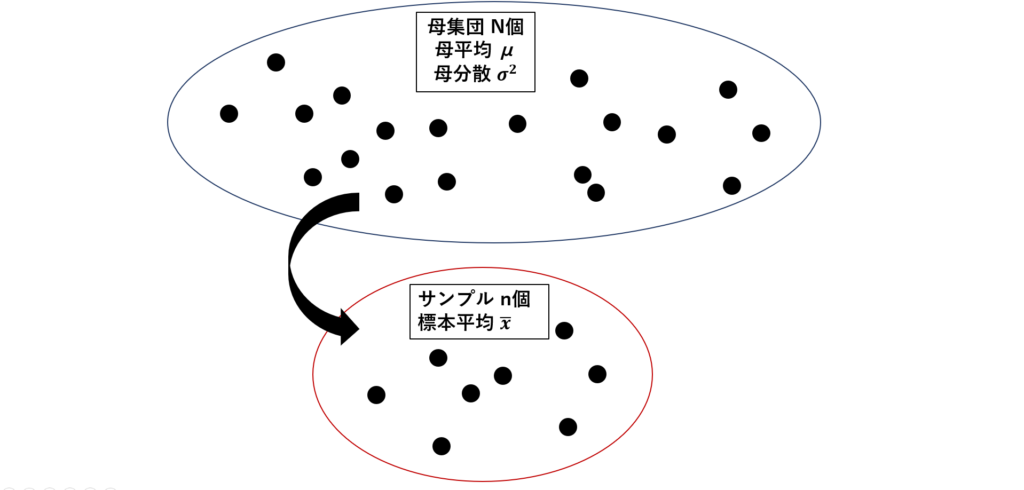
まず、ランダムサンプリングとは、母集団全てを調べることが難しいため母集団を忠実に表すサンプリングを作るようサンプリングすることです。
図示すると下記のようになります。
母集団N個を全て調べるのが難しいから、調べられるn個を無作為に抽出して調べることで母集団の傾向を掴もうとすることです。
このとき、無作為にサンプリングしたn個の平均値の期待値と分散は次のように表せられます。
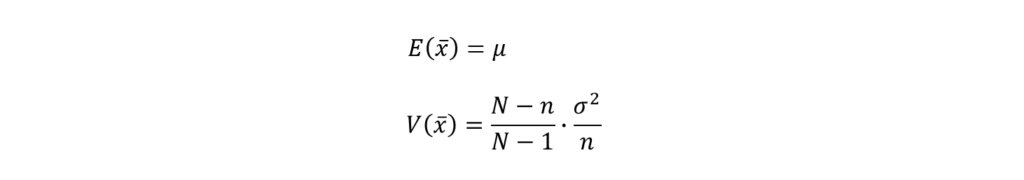
では、なぜこう表せるかを考えていきましょう！
平均値の期待値の導出
まずは、平均値の期待値から導出していきます。
はい、導出できましたね！
平均値の分散の導出
まず、（N－n）/(N-1)は母集団からサンプルをとっていく中で徐々に母集団の数が減っていくことを表すための有限修正と呼ばれるものです。
どうやって、この値が出てきたの？と疑問に感じた方は、「超幾何分布とは（1)」において超幾何分布の分散導出で解説してますので参照ください。
母集団が抜き取り個数に対して十分に大きければ、(N-n)/(N-1)が1に近づくことがわかるように有限修正は無視できます。
一般的には、
抜き取り比n/Nが0.5より大きい場合は大きく効いてくる。
抜き取り比n/Nが0.1より小さい場合は無限母集団とみなしてよい。
とされています。
導出過程は下記のようになります。
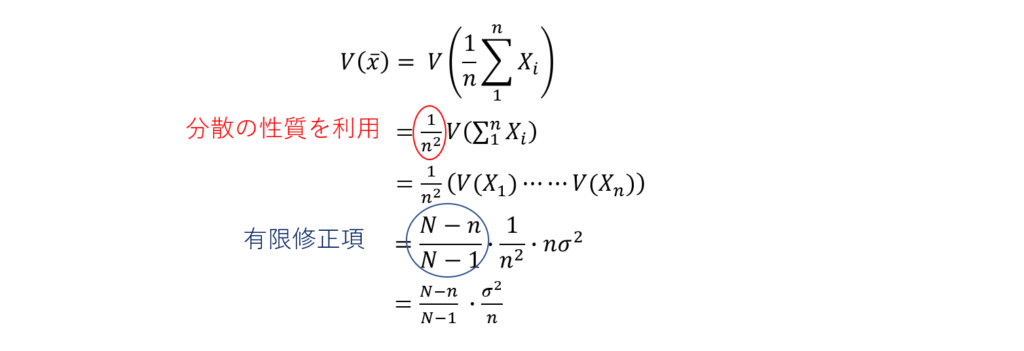
導出過程内で、分散の性質を利用しましたが何これ？と思った方のために紹介しておきます。
用いた分散の性質はこちらです！
（分散の性質の導出過程も書いておきます）
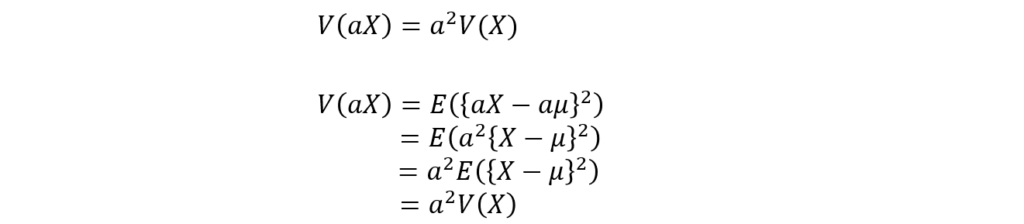
以上で、ランダムサンプリングの平均値の期待値と分散を導出できましたね！
追求すれば、どんどん新しい知識を学べることが実感していただけたのではないでしょうか。
おすすめ学習教材
最後にですが、私が学習に使用した教材を紹介しておきます。
①過去問（直近2冊 計8回分） 約5,000円
②QC検定受験テキスト1級 約5,000円
③品質管理の演習問題と解説QC検定1級 約5,000円
コメント